Skip to contents

Analyse fading measurements and returns the fading rate per decade (g-value)

Source: R/analyse_FadingMeasurement.R
analyse_FadingMeasurement.Rd

The function analysis fading measurements and returns a fading rate including an error estimation. The function is not limited to standard fading measurements, as can be seen, e.g., Huntley and Lamothe (2001). Additionally, the density of recombination centres (rho') is estimated after Kars et al. (2008).

Usage

analyse_FadingMeasurement(
  object,
  structure = c("Lx", "Tx"),
  signal.integral,
  background.integral,
  t_star = "half",
  n.MC = 100,
  verbose = TRUE,
  plot = TRUE,
  plot.single = FALSE,
  ...
)

Arguments

object

RLum.Analysis (required): input object with the measurement data. Alternatively, a list containing RLum.Analysis objects or a data.frame with three columns (x = LxTx, y = LxTx error, z = time since irradiation) can be provided. Can also be a wide table, i.e. a data.frame with a number of columns divisible by 3 and where each triplet has the before mentioned column structure.

Please note: The input object should solely consists of the curve needed for the data analysis, i.e. only IRSL curves representing Lx (and Tx)

If data from multiple aliquots are provided please see the details below with regard to Lx/Tx normalisation. The function assumes that all your measurements are related to one (comparable) sample. If you have to treat independent samples, you have use this function in a loop.

structure

character (with default): sets the structure of the measurement data. Allowed are 'Lx' or c('Lx','Tx'). Other input is ignored

signal.integral

vector (required): vector with channels for the signal integral (e.g., c(1:10)). Not required if a data.frame with LxTx values is provided.

background.integral

vector (required): vector with channels for the background integral (e.g., c(90:100)). Not required if a data.frame with LxTx values is provided.

t_star

character (with default): method for calculating the time elapsed since irradiation if input is not a data.frame. Options are: 'half' (the default), 'half_complex, which uses the long equation in Auclair et al. 2003, and and 'end', which takes the time between irradiation and the measurement step. Alternatively, t_star can be a function with one parameter which works on t1. For more information see details.

t_star has no effect if the input is a data.frame, because this input comes without irradiation times.

n.MC

integer (with default): number for Monte Carlo runs for the error estimation

verbose

logical (with default): enables/disables verbose mode

plot

logical (with default): enables/disables plot output

plot.single

logical (with default): enables/disables single plot mode, i.e. one plot window per plot. Alternatively a vector specifying the plot to be drawn, e.g., plot.single = c(3,4) draws only the last two plots

...

(optional) further arguments that can be passed to internally used functions. Supported arguments: xlab, log, mtext, plot.trend (enable/disable trend blue line), and xlim for the two first curve plots, and ylim for the fading curve plot. For further plot customization please use the numerical output of the functions for own plots.

Value

An RLum.Results object is returned:

Slot: @data

OBJECTTYPECOMMENT
fading_resultsdata.frameresults of the fading measurement in a table
fitlmobject returned by the used linear fitting function stats::lm
rho_primedata.frameresults of rho' estimation after Kars et al. (2008)
LxTx_tabledata.frameLx/Tx table, if curve data had been provided
irr.timesintegervector with the irradiation times in seconds

Slot: @info

OBJECTTYPECOMMENT
callcallthe original function call

Details

All provided output corresponds to the \(tc\) value obtained by this analysis. Additionally in the output object the g-value normalised to 2-days is provided. The output of this function can be passed to the function calc_FadingCorr.

Fitting and error estimation

For the fitting the function stats::lm is used without applying weights. For the error estimation all input values, except tc, as the precision can be considered as sufficiently high enough with regard to the underlying problem, are sampled assuming a normal distribution for each value with the value as the mean and the provided uncertainty as standard deviation.

The options for t_star

  • t_star = "half" (the default) The calculation follows the simplified version in Auclair et al. (2003), which reads $$t_{star} := t_1 + (t_2 - t_1)/2$$

  • t_star = "half_complex" This option applies the complex function shown in Auclair et al. (2003), which is derived from Aitken (1985) appendix F, equations 9 and 11. It reads $$t_{star} = t0 * 10^[(t_2 log(t_2/t_0) - t_1 log(t_1/t_0) - 0.43(t_2 - t_1))/(t_2 - t_1)]$$ where 0.43 = \(1/ln(10)\). t0, which is an arbitrary constant, is set to 1. Please note that the equation in Auclair et al. (2003) is incorrect insofar that it reads \(10exp(...)\), where the base should be 10 and not the Euler's number. Here we use the correct version (base 10).

  • t_star = "end" This option uses the simplest possible form for t_star which is the time since irradiation without taking into account any addition parameter and it equals t1 in Auclair et al. (2003)

  • t_star = <function> This last option allows you to provide an R function object that works on t1 and gives you all possible freedom. For instance, you may want to define the following function fun <- function(x) {x^2}, this would square all values of t1, because internally it calls fun(t1). The name of the function does not matter.

Density of recombination centres

The density of recombination centres, expressed by the dimensionless variable rho', is estimated by fitting equation 5 in Kars et al. (2008) to the data. For the fitting the function stats::nls is used without applying weights. For the error estimation the same procedure as for the g-value is applied (see above).

Multiple aliquots & Lx/Tx normalisation

Be aware that this function will always normalise all \(\frac{L_x}{T_x}\) values by the \(\frac{L_x}{T_x}\) value of the prompt measurement of the first aliquot. This implicitly assumes that there are no systematic inter-aliquot variations in the \(\frac{L_x}{T_x}\) values. If deemed necessary to normalise the \(\frac{L_x}{T_x}\) values of each aliquot by its individual prompt measurement please do so before running analyse_FadingMeasurement and provide the already normalised values for object instead.

Shine-down curve plots Please note that the shine-down curve plots are for information only. As such not all pause steps are plotted to avoid graphically overloaded plots. However, all pause times are taken into consideration for the analysis.

Function version

0.1.22

How to cite

Kreutzer, S., Burow, C., 2024. analyse_FadingMeasurement(): Analyse fading measurements and returns the fading rate per decade (g-value). Function version 0.1.22. In: Kreutzer, S., Burow, C., Dietze, M., Fuchs, M.C., Schmidt, C., Fischer, M., Friedrich, J., Mercier, N., Philippe, A., Riedesel, S., Autzen, M., Mittelstrass, D., Gray, H.J., Galharret, J., Colombo, M., 2024. Luminescence: Comprehensive Luminescence Dating Data Analysis. R package version 0.9.26. https://r-lum.github.io/Luminescence/

References

Aitken, M.J., 1985. Thermoluminescence dating, Studies in archaeological science. Academic Press, London, Orlando.

Auclair, M., Lamothe, M., Huot, S., 2003. Measurement of anomalous fading for feldspar IRSL using SAR. Radiation Measurements 37, 487-492. doi:10.1016/S1350-4487(03)00018-0

Huntley, D.J., Lamothe, M., 2001. Ubiquity of anomalous fading in K-feldspars and the measurement and correction for it in optical dating. Canadian Journal of Earth Sciences 38, 1093-1106. doi: 10.1139/cjes-38-7-1093

Kars, R.H., Wallinga, J., Cohen, K.M., 2008. A new approach towards anomalous fading correction for feldspar IRSL dating-tests on samples in field saturation. Radiation Measurements 43, 786-790. doi:10.1016/j.radmeas.2008.01.021

See also

calc_OSLLxTxRatio, read_BIN2R, read_XSYG2R, extract_IrradiationTimes, calc_FadingCorr

Author

Sebastian Kreutzer, Institute of Geography, Heidelberg University (Germany)
Christoph Burow, University of Cologne (Germany) , RLum Developer Team

Examples


## load example data (sample UNIL/NB123, see ?ExampleData.Fading)
data("ExampleData.Fading", envir = environment())

##(1) get fading measurement data (here a three column data.frame)
fading_data <- ExampleData.Fading$fading.data$IR50

##(2) run analysis
g_value <- analyse_FadingMeasurement(
fading_data,
plot = TRUE,
verbose = TRUE,
n.MC = 10)

#> 
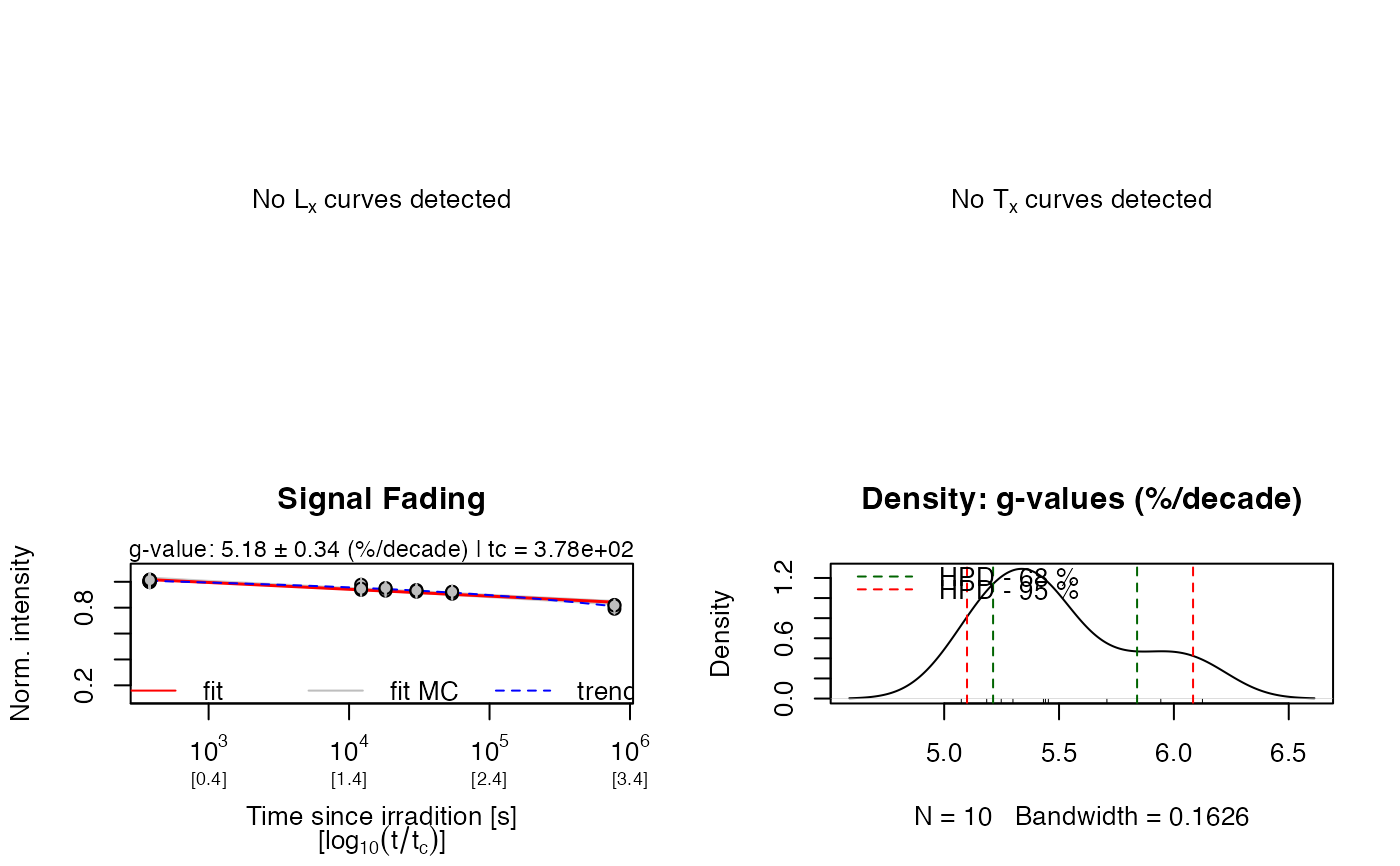#> [analyse_FadingMeasurement()]
#> 
#>  n.MC:	10
#>  tc:	3.78e+02 s
#> ---------------------------------------------------
#> T_0.5 interpolated:	NA
#> T_0.5 predicted:	4e+11
#> g-value:		5.18 ± 0.34 (%/decade)
#> g-value (norm. 2 days):	6.01 ± 0.34 (%/decade)
#> ---------------------------------------------------
#> rho':			3.93e-06 ± 3.81e-07
#> log10(rho'):		-5.41 ± 0.04
#> ---------------------------------------------------

##(3) this can be further used in the function
## to correct the age according to Huntley & Lamothe, 2001
results <- calc_FadingCorr(
age.faded = c(100,2),
g_value = g_value,
n.MC = 10)
#> 
#> 
#> [calc_FadingCorr()]
#> 
#>  >> Fading correction according to Huntley & Lamothe (2001)
#> 
#>  .. used g-value:	5.182 ± 0.337 %/decade
#>  .. used tc:		1.198e-08 ka
#>  .. used kappa:		0.0225 ± 0.0015
#>  ----------------------------------------------
#>  seed: 			NA
#>  n.MC: 			10
#>  observations: 		10
#>  ----------------------------------------------
#>  Age (faded):		100 ka ± 2 ka
#>  Age (corr.):		203.0812 ka ± 13.4105 ka
#>  ----------------------------------------------