Fitting and Deconvolution of OSL Lifetime Components

Usage

fit_OSLLifeTimes(
  object,
  tp = 0,
  signal_range = NULL,
  n.components = NULL,
  method_control = list(),
  plot = TRUE,
  plot_simple = FALSE,
  verbose = TRUE,
  ...
)

Arguments

object: RLum.Data.Curve, RLum.Analysis, data.frame or matrix (required): Input object containing the data to be analysed. All objects can be provided also as list for an automated processing. Please note: NA values are automatically removed and the dataset should comprise at least 5 data points (possibly more if n.components is set to a value greater than 1)
tp: numeric (with default): option to account for the stimulation pulse width. For off-time measurements the default value is 0. tp has the same unit as the measurement data, e.g., µs. Please set this parameter carefully, if it all, otherwise you may heavily bias your fit results.
signal_range: numeric (optional): allows to set a channel range, by default all channels are used, e.g. signal_range = c(2,100) considers only channels 2 to 100 and signal_range = c(2) considers only channels from channel 2 onwards.
n.components: numeric (optional): Fix the number of components. If set the algorithm will try to fit the number of predefined components. If nothing is set, the algorithm will try to find the best number of components.
method_control: list (optional): Named to allow a more fine control of the fitting process. See details for allowed options.
plot: logical (with default): Enable/disable plot output
plot_simple: logical (with default): Enable/disable reduced plot output. If TRUE, no residual plot is shown, however, plot output can be combined using the standard R layout options, such as par(mfrow = c(2,2)).
verbose: logical (with default): Enable/disable terminal feedback
...: parameters passed to plot.default to control the plot output, supported are: main, xlab, ylab, log, xlim, ylim, col, lty, legend.pos, legend.text. If the input object is of type RLum.Analysis this arguments can be provided as a list.

Value

———————————–
[ NUMERICAL OUTPUT ]
———————————–

RLum.Results-object

slot: @data

Element	Type	Description
`$data`	`matrix`	the final fit matrix
`$start_matrix`	`matrix`	the start matrix used for the fitting
`$total_counts`	`integer`	Photon count sum
`$fit`	`nls`	the fit object returned by minpack.lm::nls.lm

slot: @info

The original function call

————————
[ TERMINAL OUTPUT ]
————————

Terminal output is only shown of the argument verbose = TRUE.

(1) Start parameter and component adaption
Trave of the parameter adaptation process

(2) Fitting results (sorted by ascending tau)
The fitting results sorted by ascending tau value. Please note that if you access the nls fitting object, the values are not sorted.

(3) Further information

The photon count sum
Durbin-Watson residual statistic to asses whether the residuals are correlated, ideally the residuals should be not correlated at all. Rough measures are:
D = 0: the residuals are systematically correlated
D = 2: the residuals are randomly distributed
D = 4: the residuals are systematically anti-correlated

You should be suspicious if D differs largely from 2.

————————
[ PLOT OUTPUT ]
————————

A plot showing the original data and the fit so far possible. The lower plot shows the residuals of the fit.

Details

The function intends to provide an easy access to pulsed optically stimulated luminescence (POSL) data, in order determine signal lifetimes. The fitting is currently optimised to work with the off-time flank of POSL measurements only. For the signal deconvolution, a differential evolution optimisation is combined with nonlinear least-square fitting following the approach by Bluszcz & Adamiec (2006).

Component deconvolution algorithm

The component deconvolution consists of two steps:

(1) Adaptation phase

In the adaptation phase the function tries to figure out the optimal and statistically justified number of signal components following roughly the approach suggested by Bluszcz & Adamiec (2006). In contrast to their work, for the optimisation by differential evolution here the package 'DEoptim' is used.

The function to be optimized has the form:

$$\chi^2 = \sum(w * (n_i/c - \sum(A_i * exp(-x/(tau_i + t_p))))^2)$$

with $w = 1$ for unweighted regression analysis (method_control = list(weights = FALSE)) or $w = c^2/n_i$ for weighted regression analysis. The default values is TRUE.

$$F = (\Delta\chi^2 / 2) / (\chi^2/(N - 2*m - 2))$$

(2) Final fitting

method_control

Parameter	Type	Description
`p`	numeric	controls the probability for the F statistic reference values. For a significance level of 5 % a value of 0.95 (the default) should be added, for 1 %, a value of 0.99 is sufficient: 1 > p > 0 (cf. stats::FDist)
`seed`	numeric	set the seed for the random number generator, provide a value here to get reproducible results
`DEoptim.trace`	logical	enables/disables the tracing of the differential evolution (cf. DEoptim::DEoptim.control)
`DEoptim.itermax`	logical	controls the number of the allowed generations (cf. DEoptim::DEoptim.control)
`weights`	logical	enables/disables the weighting for the start parameter estimation and fitting (see equations above). The default values is `TRUE`
`nlsLM.trace`	logical	enables/disables trace mode for the nls fitting (minpack.lm::nlsLM), can be used to identify convergence problems, default is `FALSE`
`nlsLM.upper`	logical	enables/disables upper parameter boundary, default is `TRUE`
`nlsLM.lower`	logical	enables/disables lower parameter boundary, default is `TRUE`

Function version

0.1.5

How to cite

Kreutzer, S., Schmidt, C., 2024. fit_OSLLifeTimes(): Fitting and Deconvolution of OSL Lifetime Components. Function version 0.1.5. In: Kreutzer, S., Burow, C., Dietze, M., Fuchs, M.C., Schmidt, C., Fischer, M., Friedrich, J., Mercier, N., Philippe, A., Riedesel, S., Autzen, M., Mittelstrass, D., Gray, H.J., Galharret, J., Colombo, M., 2024. Luminescence: Comprehensive Luminescence Dating Data Analysis. R package version 0.9.26. https://r-lum.github.io/Luminescence/

References

Bluszcz, A., Adamiec, G., 2006. Application of differential evolution to fitting OSL decay curves. Radiation Measurements 41, 886-891. doi:10.1016/j.radmeas.2006.05.016

Durbin, J., Watson, G.S., 1950. Testing for Serial Correlation in Least Squares Regression: I. Biometrika 37, 409-21. doi:10.2307/2332391

Further reading

Hughes, I., Hase, T., 2010. Measurements and Their Uncertainties. Oxford University Press.

Storn, R., Price, K., 1997. Differential Evolution – A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization 11, 341–359.

Author

Sebastian Kreutzer, Geography & Earth Sciences, Aberystwyth University, Christoph Schmidt, University of Bayreuth (Germany) , RLum Developer Team

Examples


##load example data
data(ExampleData.TR_OSL, envir = environment())

##fit lifetimes (short run)
fit_OSLLifeTimes(
 object = ExampleData.TR_OSL,
 n.components = 1)
#> 
#> [fit_OSLLifeTime()]
#> 
#> (1) Start parameter and component adapation
#> ---------------------(start adaption)------------------------------------
#> >> + adaption for 1 comp. :  Inf (calc.) <>  3 (ref.) >> [add comp.] >> [forced stop]
#> ---------------------(end adaption)--------------------------------------
#> 
#> 
#> >> Applied component matrix
#>                   A     tau
#> Comp.1 2.118737e+12 87.9146
#> 
#> 
#> (2) Fitting results (sorted by ascending tau)
#> -------------------------------------------------------------------------
#>           Estimate   Std. Error   t value      Pr(>|t|)
#> A.1   2.118737e+10 9.710554e+07 218.18915  0.000000e+00
#> tau.1 8.791461e+01 3.167935e+00  27.75139 1.196536e-143
#> -------------------------------------------------------------------------
#> 
#> (3) Further information
#> -------------------------------------------------------------------------
#> Photon count sum:  3.831e+13 
#> Durbin-Watson residual statistic:  0.77 [ <>        ]
#> 

#> 
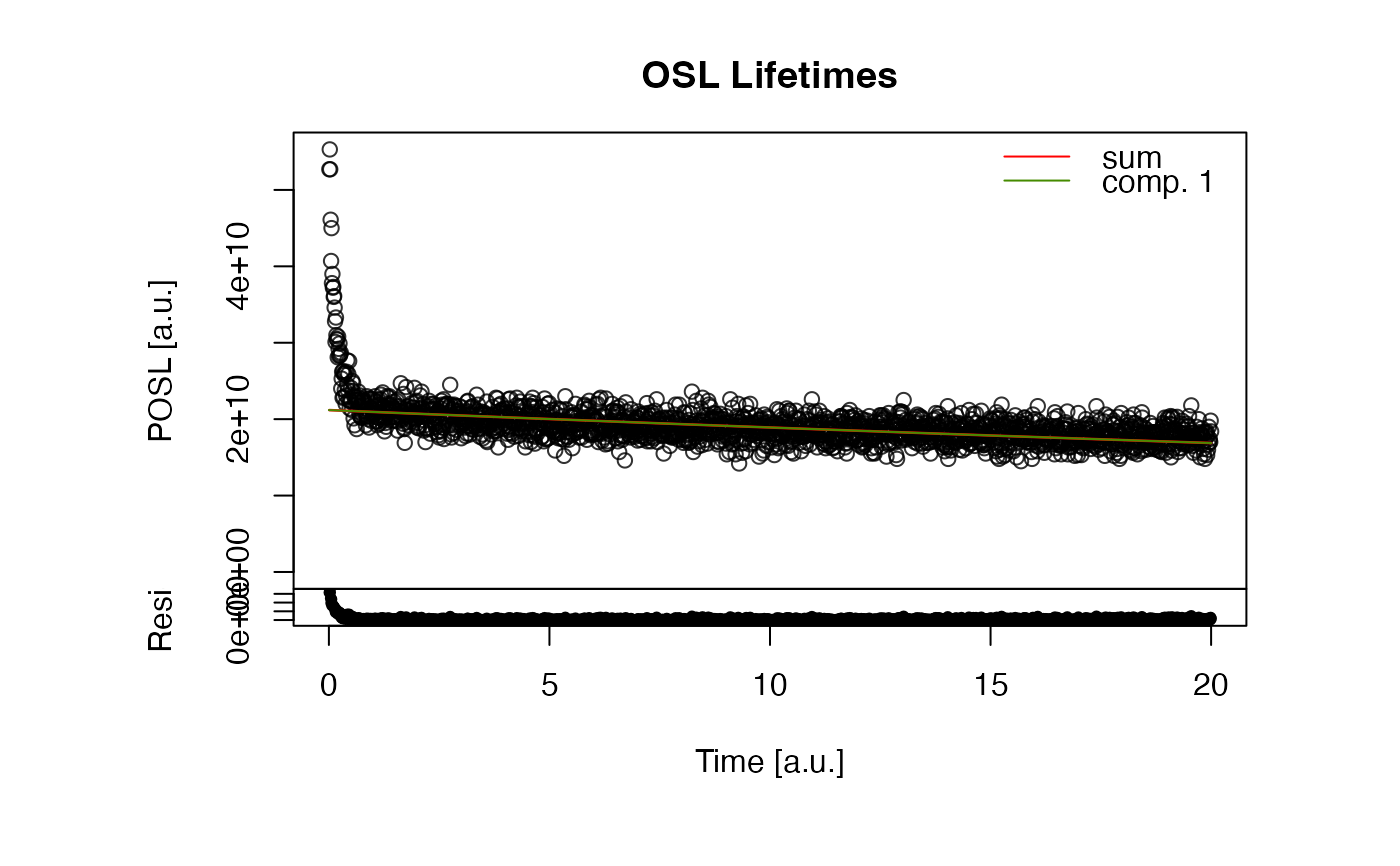#>  [RLum.Results-class]
#> 	 originator: fit_OSLLifeTimes()
#> 	 data: 4
#>  	 .. $data : matrix
#> 	 .. $start_matrix : matrix
#> 	 .. $total_counts : numeric
#> 	 .. $fit : nls
#> 	 additional info elements:  1 

##long example
if (FALSE) { # \dontrun{
fit_OSLLifeTimes(
object = ExampleData.TR_OSL)
} # }