Skip to contents

Transform a CW-OSL curve into a pLM-OSL curve via interpolation under linear modulation conditions

Source: R/CW2pLMi.R
CW2pLMi.Rd

Transforms a conventionally measured continuous-wave (CW) OSL-curve into a pseudo linearly modulated (pLM) curve under linear modulation conditions using the interpolation procedure described by Bos & Wallinga (2012).

Usage

CW2pLMi(values, P)

Arguments

values

RLum.Data.Curve or data.frame (required): RLum.Data.Curve or data.frame with measured curve data of type stimulation time (t) (values[,1]) and measured counts (cts) (values[,2])

P

vector (optional): stimulation time in seconds. If no value is given the optimal value is estimated automatically (see details). Greater values of P produce more points in the rising tail of the curve.

Value

The function returns the same data type as the input data type with the transformed curve values.

RLum.Data.Curve

$CW2pLMi.x.t: transformed time values
$CW2pLMi.method: used method for the production of the new data points

Details

The complete procedure of the transformation is given in Bos & Wallinga (2012). The input data.frame consists of two columns: time (t) and count values (CW(t))

Nomenclature

  • P = stimulation time (s)

  • 1/P = stimulation rate (1/s)

Internal transformation steps

(1) log(CW-OSL) values

(2) Calculate t' which is the transformed time: $$t' = 1/2*1/P*t^2$$

(3) Interpolate CW(t'), i.e. use the log(CW(t)) to obtain the count values for the transformed time (t'). Values beyond min(t) and max(t) produce NA values.

(4) Select all values for t' < min(t), i.e. values beyond the time resolution of t. Select the first two values of the transformed data set which contain no NA values and use these values for a linear fit using lm.

(5) Extrapolate values for t' < min(t) based on the previously obtained fit parameters.

(6) Transform values using $$pLM(t) = t/P*CW(t')$$

(7) Combine values and truncate all values for t' > max(t)

NOTE: The number of values for t' < min(t) depends on the stimulation period (P) and therefore on the stimulation rate 1/P. To avoid the production of too many artificial data at the raising tail of the determined pLM curves it is recommended to use the automatic estimation routine for P, i.e. provide no own value for P.

Note

According to Bos & Wallinga (2012) the number of extrapolated points should be limited to avoid artificial intensity data. If P is provided manually and more than two points are extrapolated, a warning message is returned.

Function version

0.3.1

How to cite

Kreutzer, S., 2024. CW2pLMi(): Transform a CW-OSL curve into a pLM-OSL curve via interpolation under linear modulation conditions. Function version 0.3.1. In: Kreutzer, S., Burow, C., Dietze, M., Fuchs, M.C., Schmidt, C., Fischer, M., Friedrich, J., Mercier, N., Philippe, A., Riedesel, S., Autzen, M., Mittelstrass, D., Gray, H.J., Galharret, J., Colombo, M., 2024. Luminescence: Comprehensive Luminescence Dating Data Analysis. R package version 0.9.26. https://r-lum.github.io/Luminescence/

References

Bos, A.J.J. & Wallinga, J., 2012. How to visualize quartz OSL signal components. Radiation Measurements, 47, 752-758.

Further Reading

Bulur, E., 1996. An Alternative Technique For Optically Stimulated Luminescence (OSL) Experiment. Radiation Measurements, 26, 701-709.

Bulur, E., 2000. A simple transformation for converting CW-OSL curves to LM-OSL curves. Radiation Measurements, 32, 141-145.

See also

CW2pLM, CW2pHMi, CW2pPMi, fit_LMCurve, RLum.Data.Curve

Author

Sebastian Kreutzer, Institute of Geography, Heidelberg University (Germany)

Based on comments and suggestions from:
Adrie J.J. Bos, Delft University of Technology, The Netherlands , RLum Developer Team

Examples


##(1)
##load CW-OSL curve data
data(ExampleData.CW_OSL_Curve, envir = environment())

##transform values
values.transformed <- CW2pLMi(ExampleData.CW_OSL_Curve)

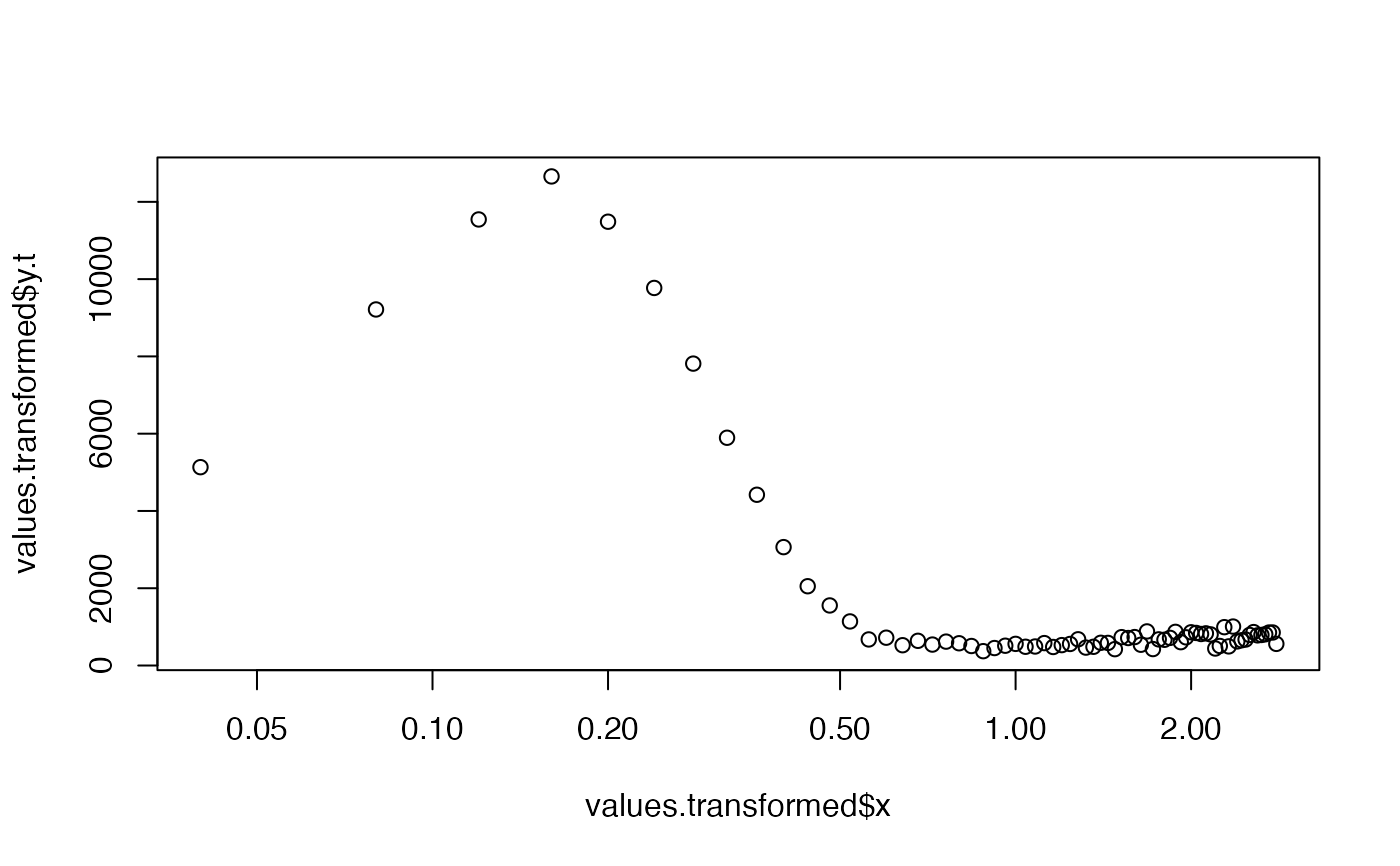
##plot
plot(values.transformed$x, values.transformed$y.t, log = "x")


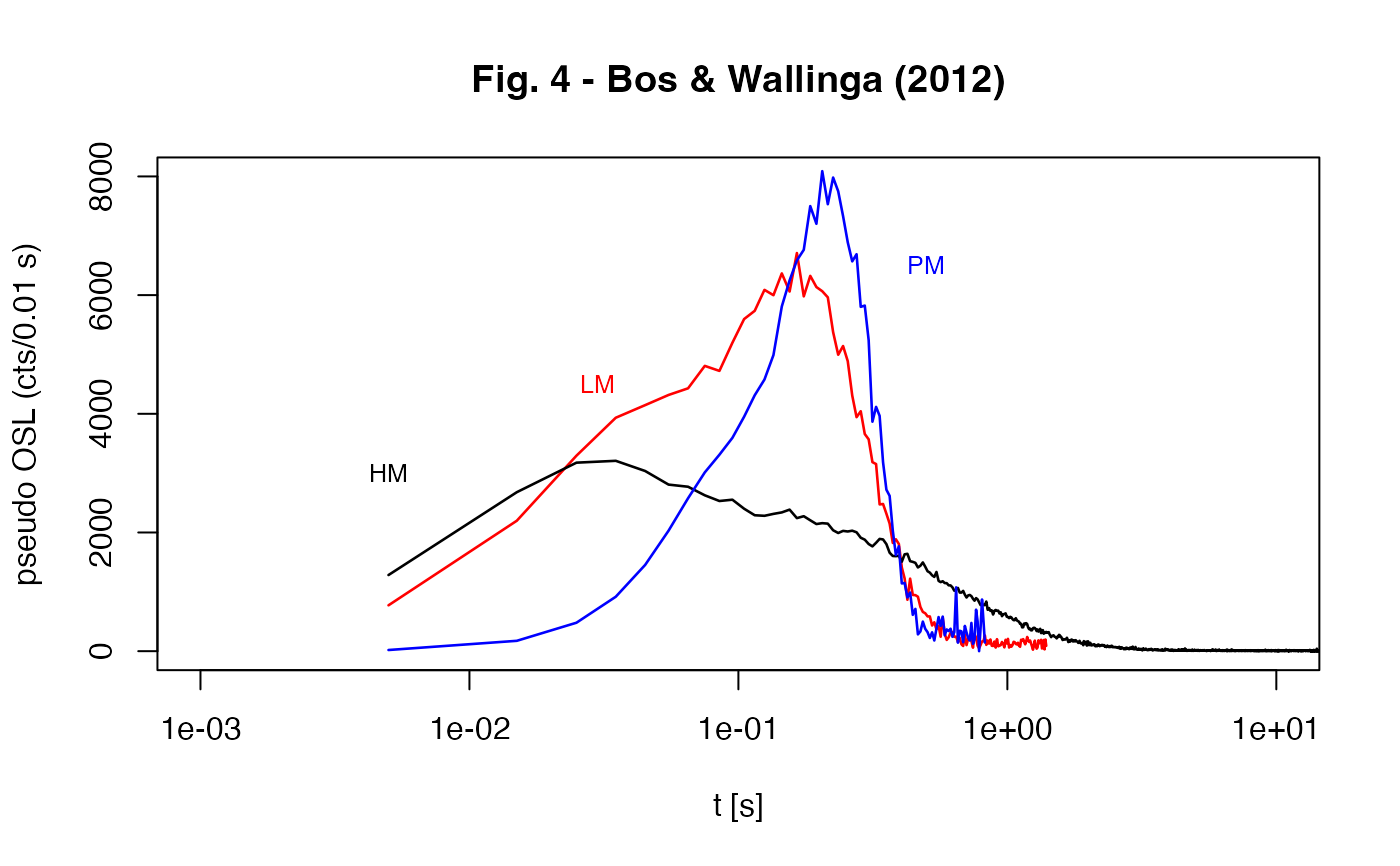
##(2) - produce Fig. 4 from Bos & Wallinga (2012)
##load data
data(ExampleData.CW_OSL_Curve, envir = environment())
values <- CW_Curve.BosWallinga2012

##open plot area
plot(NA, NA,
     xlim = c(0.001,10),
     ylim = c(0,8000),
     ylab = "pseudo OSL (cts/0.01 s)",
     xlab = "t [s]",
     log = "x",
     main = "Fig. 4 - Bos & Wallinga (2012)")


values.t <- CW2pLMi(values, P = 1/20)
lines(values[1:length(values.t[,1]),1],CW2pLMi(values, P = 1/20)[,2],
      col = "red", lwd = 1.3)
text(0.03,4500,"LM", col = "red", cex = .8)

values.t <- CW2pHMi(values, delta = 40)
#> Warning: [CW2pHMi()] 56 values have been found and replaced by the mean of the nearest values
lines(values[1:length(values.t[,1]),1],CW2pHMi(values, delta = 40)[,2],
      col = "black", lwd = 1.3)
#> Warning: [CW2pHMi()] 56 values have been found and replaced by the mean of the nearest values
text(0.005,3000,"HM", cex =.8)

values.t <- CW2pPMi(values, P = 1/10)
#> Warning: t' is beyond the time resolution. Only two data points have been extrapolated, the first 3 points have been set to 0!
lines(values[1:length(values.t[,1]),1], CW2pPMi(values, P = 1/10)[,2],
      col = "blue", lwd = 1.3)
#> Warning: t' is beyond the time resolution. Only two data points have been extrapolated, the first 3 points have been set to 0!
text(0.5,6500,"PM", col = "blue", cex = .8)