Function to calculate statistic measures — calc

This function calculates a number of descriptive statistics for estimates with a given standard error (SE), most fundamentally using error-weighted approaches.

Usage

calc_Statistics(
  data,
  weight.calc = "square",
  digits = NULL,
  n.MCM = NULL,
  na.rm = TRUE
)

Arguments

data: data.frame or RLum.Results object (required): for data.frame two columns: De (data[, 1]) and De error (data[, 2]).
weight.calc: character (with default): type of weight calculation. One out of "reciprocal" (weight is 1/error), "square" (weight is 1/error^2). Default is "square".
digits: integer (with default): number of decimal places to be used when rounding numbers. If set to NULL (default), no rounding occurs.
n.MCM: numeric (with default): number of samples drawn for Monte Carlo-based statistics. NULL (the default) disables MC runs.
na.rm: logical (with default): indicating whether NA values should be stripped before the computation proceeds.

Value

Returns a list with weighted and unweighted statistic measures.

Details

The option to use Monte Carlo Methods (n.MCM) allows calculating all descriptive statistics based on random values. The distribution of these random values is based on the Normal distribution with De values as means and De_error values as one standard deviation. Increasing the number of MCM-samples linearly increases computation time. On a Lenovo X230 machine evaluation of 25 Aliquots with n.MCM = 1000 takes 0.01 s, with n = 100000, ca. 1.65 s. It might be useful to work with logarithms of these values. See Dietze et al. (2016, Quaternary Geochronology) and the function plot_AbanicoPlot for details.

Function version

0.1.7

Author

Michael Dietze, GFZ Potsdam (Germany) , RLum Developer Team

How to cite

Dietze, M., 2025. calc_Statistics(): Function to calculate statistic measures. Function version 0.1.7. In: Kreutzer, S., Burow, C., Dietze, M., Fuchs, M.C., Schmidt, C., Fischer, M., Friedrich, J., Mercier, N., Philippe, A., Riedesel, S., Autzen, M., Mittelstrass, D., Gray, H.J., Galharret, J., Colombo, M., Steinbuch, L., Boer, A.d., 2025. Luminescence: Comprehensive Luminescence Dating Data Analysis. R package version 1.1.1. https://r-lum.github.io/Luminescence/

Examples


## load example data
data(ExampleData.DeValues, envir = environment())

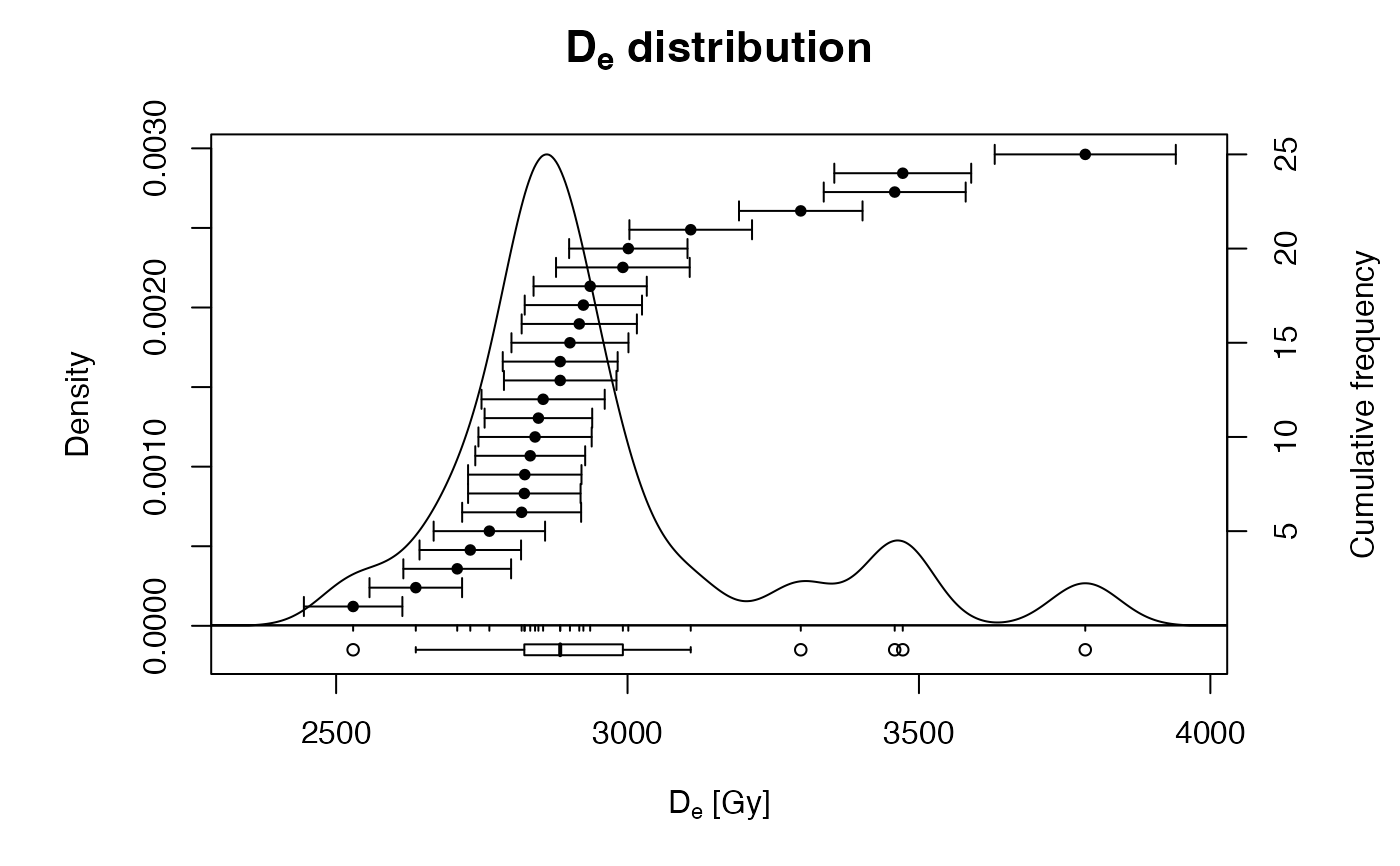
## show a rough plot of the data to illustrate the non-normal distribution
plot_KDE(ExampleData.DeValues$BT998)


## calculate statistics and show output
str(calc_Statistics(ExampleData.DeValues$BT998))
#> List of 3
#>  $ weighted  :List of 9
#>   ..$ n       : int 25
#>   ..$ mean    : num 2896
#>   ..$ median  : num 2847
#>   ..$ sd.abs  : num 240
#>   ..$ sd.rel  : num 8.29
#>   ..$ se.abs  : num 48
#>   ..$ se.rel  : num 1.66
#>   ..$ skewness: num 1.34
#>   ..$ kurtosis: num 4.39
#>  $ unweighted:List of 9
#>   ..$ n       : int 25
#>   ..$ mean    : num 2951
#>   ..$ median  : num 2884
#>   ..$ sd.abs  : num 282
#>   ..$ sd.rel  : num 9.54
#>   ..$ se.abs  : num 56.3
#>   ..$ se.rel  : num 1.91
#>   ..$ skewness: num 1.34
#>   ..$ kurtosis: num 4.39
#>  $ MCM       :List of 9
#>   ..$ n       : int 25
#>   ..$ mean    : num 2951
#>   ..$ median  : num 2884
#>   ..$ sd.abs  : num 282
#>   ..$ sd.rel  : num 9.54
#>   ..$ se.abs  : num 56.3
#>   ..$ se.rel  : num 1.91
#>   ..$ skewness: num 1.34
#>   ..$ kurtosis: num 4.39

if (FALSE) { # \dontrun{
## now the same for 10000 normal distributed random numbers with equal errors
x <- as.data.frame(cbind(rnorm(n = 10^5, mean = 0, sd = 1),
                         rep(0.001, 10^5)))

## note the congruent results for weighted and unweighted measures
str(calc_Statistics(x))
} # }