Calculate De value based on the gSGC by Li et al., 2015

The function computes De value and De value error using the global standardised growth curve (gSGC) assumption proposed by Li et al., 2015 for OSL dating of sedimentary quartz.

Usage

calc_gSGC(
  data,
  gSGC.type = "0-250",
  gSGC.parameters,
  n.MC = 100,
  verbose = TRUE,
  plot = TRUE,
  ...
)

Arguments

data: data.frame (required): input data the following columns five columns in the given order: LnTn, LnTn.error, Lr1Tr1, Lr1Tr1.error, Dr1. Column names are not required.
gSGC.type: character (with default): function parameters to use for the iteration procedure, either "0-450" or "0-250", as presented in Li et al., 2015 (Table 2). This is ignored if gSGC.parameters is set.
gSGC.parameters: list (optional): option to provide own function parameters used for fitting as named list. Nomenclature follows Li et al., 2015, i.e. list(A, A.error, D0, D0.error, c, c.error, Y0, Y0.error, range), where range is defines the interval where the function is considered as valid, e.g. range = c(0,250).
If set, option gSGC.type will be ignored.
n.MC: integer (with default): number of Monte Carlo simulation runs for error estimation, see details.
verbose: logical (with default): enable/disable output to the terminal.
plot: logical (with default): enable/disable the plot output.
...: parameters will be passed to the plot output

Value

Returns an S4 object of type RLum.Results.

@data
$ De.value (data.frame)
.. $ De
.. $ De.error
.. $ Eta
$ De.MC (list) contains the matrices from the error estimation.
$ uniroot (list) contains the uniroot outputs of the De estimations

@info
`$ call“ (call) the original function call

Details

The error of the De value is determined using a Monte Carlo simulation approach. Solving of the equation is realised using uniroot. Large values for n.MC will significantly increase the computation time.

Function version

0.1.2

How to cite

Kreutzer, S., 2025. calc_gSGC(): Calculate De value based on the gSGC by Li et al., 2015. Function version 0.1.2. In: Kreutzer, S., Burow, C., Dietze, M., Fuchs, M.C., Schmidt, C., Fischer, M., Friedrich, J., Mercier, N., Philippe, A., Riedesel, S., Autzen, M., Mittelstrass, D., Gray, H.J., Galharret, J., Colombo, M., Steinbuch, L., Boer, A.d., 2025. Luminescence: Comprehensive Luminescence Dating Data Analysis. R package version 1.1.0. https://r-lum.github.io/Luminescence/

References

Li, B., Roberts, R.G., Jacobs, Z., Li, S.-H., 2015. Potential of establishing a 'global standardised growth curve' (gSGC) for optical dating of quartz from sediments. Quaternary Geochronology 27, 94-104. doi:10.1016/j.quageo.2015.02.011

Author

Sebastian Kreutzer, Institute of Geography, Heidelberg University (Germany) , RLum Developer Team

Examples


results <- calc_gSGC(data = data.frame(
LnTn =  2.361, LnTn.error = 0.087,
Lr1Tr1 = 2.744, Lr1Tr1.error = 0.091,
Dr1 = 34.4))

#> 
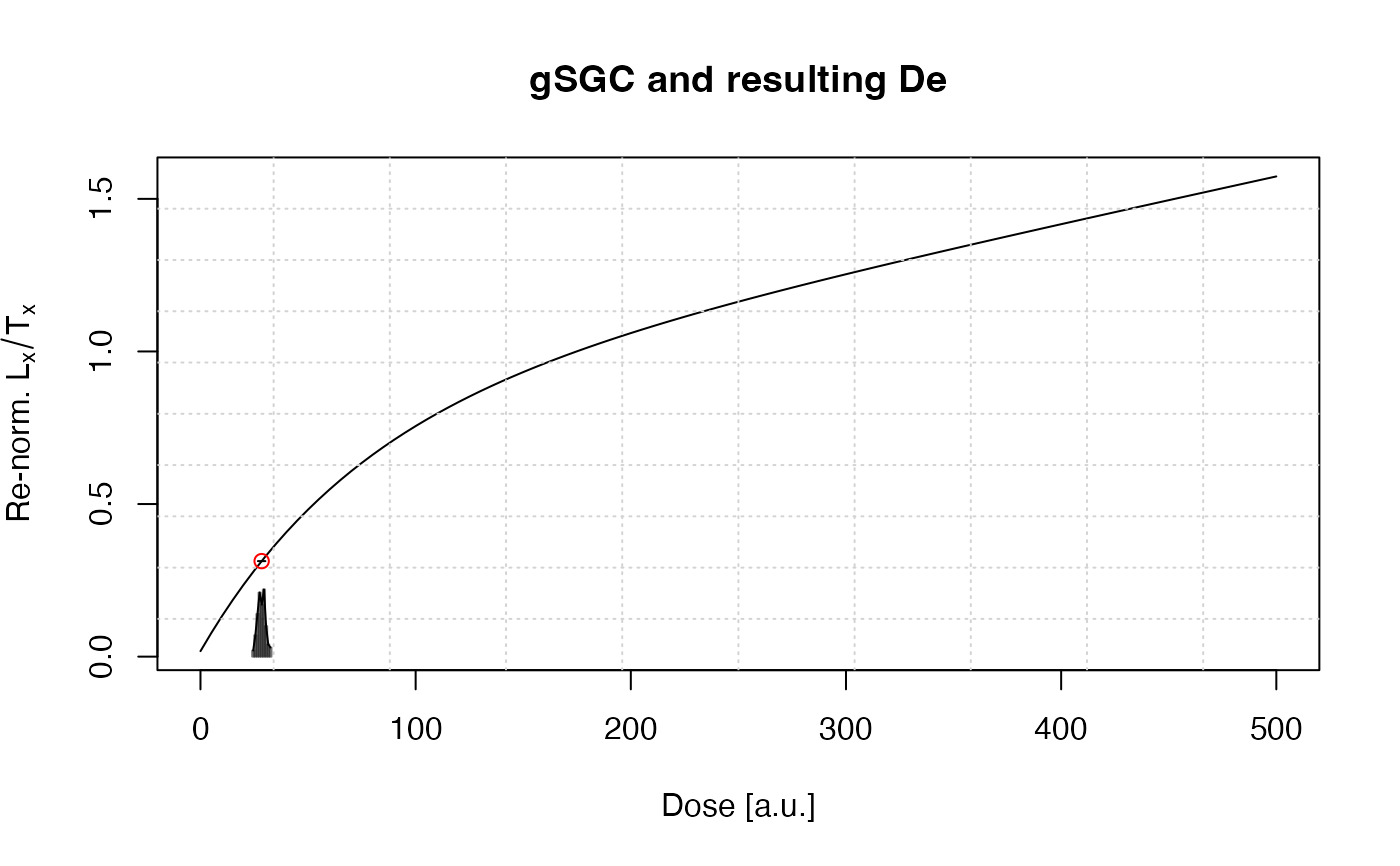#> [calc_gSGC()]
#>  Corresponding De based on the gSGC
#> 
#>  Ln/Tn:		 2.361 ± 0.087
#>  Lr1/Tr1:	 2.744 ± 0.091
#>  Dr1:		 34.4
#>  f(D):		 0.787 * (1 - exp(-D /73.9)) + c * D + 0.01791
#>  n.MC:		 100
#>  ------------------------------ 
#>  De:		28.43 ± 1.67
#>  ------------------------------ 

get_RLum(results, data.object = "De")
#>         DE DE.ERROR       ETA
#> 1 28.42881 1.665237 0.1325632