Skip to contents

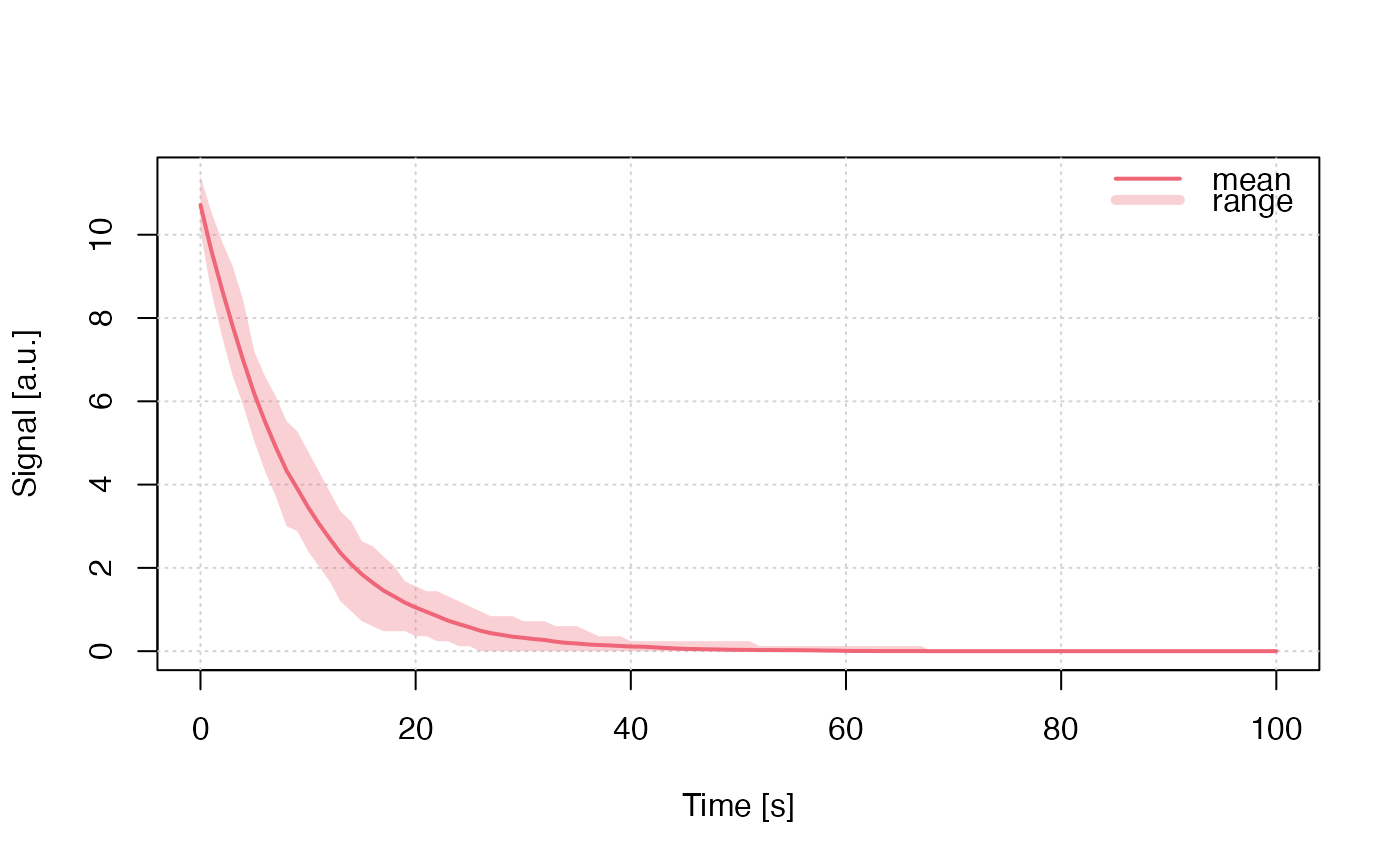
Monte-Carlo Simulation for CW-IRSL (localized transitions)

Source: R/run_MC_CW_IRSL_LOC.R
run_MC_CW_IRSL_LOC.Rd

Runs a Monte-Carlo (MC) simulation of continuous wave infrared stimulated luminescence (CW-IRSL) using the generalized one trap (GOT) model. Localized transitions refer to transitions which do not involve the conduction or valence band. These transitions take place between the ground state and an excited state of the trapped charge, and also involve an energy state of the recombination centre.

Usage

run_MC_CW_IRSL_LOC(
  A,
  times,
  clusters = 10,
  n_filled = 100,
  r,
  method = "par",
  output = "signal",
  ...
)

Arguments

A

numeric (required): The optical excitation rate from the ground state of the trap to the excited state (s^-1)

times

numeric (required): The sequence of time steps within the simulation (s)

clusters

numeric (with default): The number of created clusters for the MC runs. The input can be the output of create_ClusterSystem. In that case n_filled indicate absolute numbers of a system.

n_filled

integer (with default): The number of filled electron traps at the beginning of the simulation (dimensionless). Can be a vector of length(clusters), shorter values are recycled.

r

numeric (required): The retrapping ratio for localized transitions

method

character (with default): Sequential 'seq' or parallel 'par'processing. In the parallel mode the function tries to run the simulation on multiple CPU cores (if available) with a positive effect on the computation time.

output

character (with default): output is either the 'signal' (the default) or 'remaining_e' (the remaining charges/electrons in the trap)

...

further arguments, such as cores to control the number of used CPU cores or verbose to silence the terminal

Value

This function returns an object of class RLumCarlo_Model_Output which is a list consisting of an array with dimension length(times) x clusters and a numeric time vector.

Details

The model $$ I_{LOC}(t) = -dn/dt = A * (n^2 / (r + n)) $$

where in the function:
A := optical excitation rate from the ground state into the excited state of the trap (s^-1)
r := retrapping ratio for localized transitions
t := time (s)
n := number of filled electron traps

Function version

0.1.0

How to cite

Kreutzer, S., 2025. run_MC_CW_IRSL_LOC(): Monte-Carlo Simulation for CW-IRSL (localized transitions). Function version 0.1.0. In: Friedrich, J., Kreutzer, S., Pagonis, V., Schmidt, C., 2025. RLumCarlo: Monte-Carlo Methods for Simulating Luminescence Phenomena. R package version 0.1.10. https://r-lum.github.io/RLumCarlo/

References

Pagonis, V., Friedrich, J., Discher, M., Müller-Kirschbaum, A., Schlosser, V., Kreutzer, S., Chen, R. and Schmidt, C., 2019. Excited state luminescence signals from a random distribution of defects: A new Monte Carlo simulation approach for feldspar. Journal of Luminescence 207, 266–272. doi:10.1016/j.jlumin.2018.11.024

Further reading

Chen, R., McKeever, S.W.S., 1997. Theory of Thermoluminescence and Related Phenomena. WORLD SCIENTIFIC. doi:10.1142/2781

Author

Sebastian Kreutzer, Institute of Geography, Heidelberg University (Germany)

Examples

run_MC_CW_IRSL_LOC(
 A = 0.12,
 times = 0:100,
 clusters = 50,
 n_filled = 100,
 r = 1e-7,
 method = "seq",
 output = "signal"
) %>%
plot_RLumCarlo(legend = TRUE)