Apply the central age model (CAM) after Galbraith et al. (1999) to a given De distribution

This function calculates the central dose and dispersion of the De distribution, their standard errors and the profile log likelihood function for sigma.

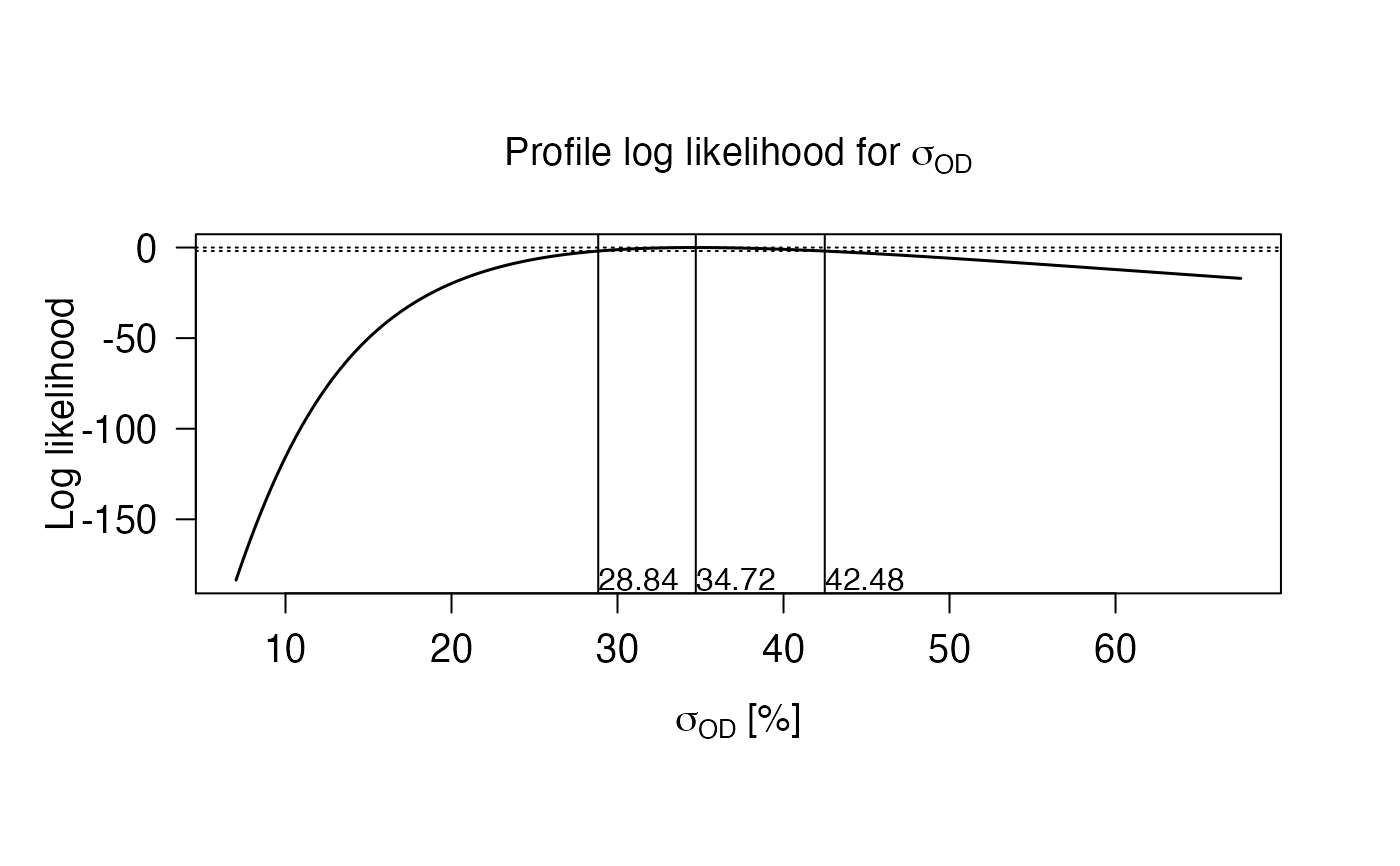
This function uses the equations of Galbraith & Roberts (2012). The parameters delta and sigma are estimated by numerically solving eq. 15 and 16. Their standard errors are approximated using eq. 17. In addition, the profile log-likelihood function for sigma is calculated using eq. 18 and presented as a plot. Numerical values of the maximum likelihood approach are only presented in the plot and not in the console. A detailed explanation on maximum likelihood estimation can be found in the appendix of Galbraith & Laslett (1993, 468-470) and Galbraith & Roberts (2012, 15)

Usage

calc_CentralDose(data, sigmab, log = TRUE, plot = TRUE, ...)

Arguments

data: RLum.Results or data.frame (required): for data.frame: two columns with De (data[,1]) and De error (data[,2]). Records containing missing values will be removed.
sigmab: numeric (with default): additional spread in De values. This value represents the expected overdispersion in the data should the sample be well-bleached (Cunningham & Walling 2012, p. 100). NOTE: For the logged model (log = TRUE) this value must be a fraction, e.g. 0.2 (= 20 %). If the un-logged model is used (log = FALSE), sigmab must be provided in the same absolute units of the De values (seconds or Gray).
log: logical (with default): fit the (un-)logged central age model to De data. Log transformation is allowed only if the De values are positive.
plot: logical (with default): enable/disable the plot output.
...: further arguments (trace, verbose).

Value

Returns a plot (optional) and terminal output. In addition an RLum.Results object is returned containing the following elements:

.$summary: data.frame summary of all relevant model results.
.$data: data.frame original input data
.$args: list used arguments
.$call: call the function call
.$profile: data.frame the log likelihood profile for sigma

The output should be accessed using the function get_RLum.

Function version

1.5

How to cite

Burow, C., 2025. calc_CentralDose(): Apply the central age model (CAM) after Galbraith et al. (1999) to a given De distribution. Function version 1.5. In: Kreutzer, S., Burow, C., Dietze, M., Fuchs, M.C., Schmidt, C., Fischer, M., Friedrich, J., Mercier, N., Philippe, A., Riedesel, S., Autzen, M., Mittelstrass, D., Gray, H.J., Galharret, J., Colombo, M., Steinbuch, L., Boer, A.d., 2025. Luminescence: Comprehensive Luminescence Dating Data Analysis. R package version 1.0.0. https://r-lum.github.io/Luminescence/

References

Galbraith, R.F. & Laslett, G.M., 1993. Statistical models for mixed fission track ages. Nuclear Tracks Radiation Measurements 4, 459-470.

Galbraith, R.F., Roberts, R.G., Laslett, G.M., Yoshida, H. & Olley, J.M., 1999. Optical dating of single grains of quartz from Jinmium rock shelter, northern Australia. Part I: experimental design and statistical models. Archaeometry 41, 339-364.

Galbraith, R.F. & Roberts, R.G., 2012. Statistical aspects of equivalent dose and error calculation and display in OSL dating: An overview and some recommendations. Quaternary Geochronology 11, 1-27.

Further reading

Arnold, L.J. & Roberts, R.G., 2009. Stochastic modelling of multi-grain equivalent dose (De) distributions: Implications for OSL dating of sediment mixtures. Quaternary Geochronology 4, 204-230.

Bailey, R.M. & Arnold, L.J., 2006. Statistical modelling of single grain quartz De distributions and an assessment of procedures for estimating burial dose. Quaternary Science Reviews 25, 2475-2502.

Cunningham, A.C. & Wallinga, J., 2012. Realizing the potential of fluvial archives using robust OSL chronologies. Quaternary Geochronology 12, 98-106.

Rodnight, H., Duller, G.A.T., Wintle, A.G. & Tooth, S., 2006. Assessing the reproducibility and accuracy of optical dating of fluvial deposits. Quaternary Geochronology, 1 109-120.

Rodnight, H., 2008. How many equivalent dose values are needed to obtain a reproducible distribution?. Ancient TL 26, 3-10.

Author

Christoph Burow, University of Cologne (Germany)
Based on a rewritten S script of Rex Galbraith, 2010 , RLum Developer Team

Examples


##load example data
data(ExampleData.DeValues, envir = environment())

##apply the central dose model
calc_CentralDose(ExampleData.DeValues$CA1)
#> 
#>  [calc_CentralDose]
#> 
#> ----------- meta data ----------------
#>  n:                       62
#>  log:                     TRUE
#> ----------- dose estimate ------------
#>  abs. central dose:       65.71
#>  abs. SE:                 3.05
#>  rel. SE [%]:             4.65
#> ----------- overdispersion -----------
#>  abs. OD:                 22.79
#>  abs. SE:                 2.27
#>  OD [%]:                  34.69
#>  SE [%]:                  3.46
#> -------------------------------------
#>